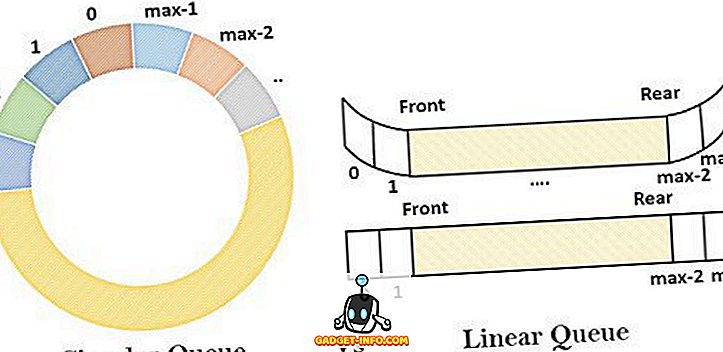
Järjekorra võib kirjeldada kui mitte-primitiivset lineaarset andmestruktuuri, mis järgib FIFO järjekorda, milles andmeelemendid sisestatakse ühest otsast (tagumine ots) ja kustutatakse teisest otsast (esiosa). Teised järjekordsed variandid on ümmargune järjekord, kahekordselt lõppenud järjekord ja prioriteedijärjekord.
Võrdluskaart
| Võrdluse alus | Lineaarne järjekord | Ümmargune järjekord |
|---|---|---|
| Põhiline | Korraldab andmeelemendid ja -juhised üksteise järel järjestuses. | Korraldab andmed ümmarguse mustriga, kus viimane element on ühendatud esimese elemendiga. |
| Ülesande täitmise kord | Ülesanded täidetakse selleks, et need oleksid eelnevalt paigutatud (FIFO). | Ülesande täitmise kord võib muutuda. |
| Sisestamine ja kustutamine | Uus element lisatakse tagumisest otsast ja eemaldatakse esiosast. | Lisamise ja kustutamise saab teha igal positsioonil. |
| Toimivus | Ebatõhus | Töötab paremini kui lineaarne järjekord. |
Lineaarse järjekorra määratlus
Lineaarne järjekord on ratsionaalselt esimene esimeses tellitud nimekirjas. Seda nimetatakse lineaarseks, kuna see sarnaneb sirgjoonega, kus elemendid paiknevad üksteise järel. See sisaldab homogeenset kogumit elementidest, milles ühele otsale lisatakse uusi elemente ja kustutatakse teisest otsast. Järjekorra mõistet saab mõista näiteks sellest, et vaatajaskond ootab väljaspool piletiloendajat, et teatripiletit saada. Selles järjekorras liitub isik pileti tagaotsas järjekorda ja pilet väljastatakse järjekorda.
Järjekorras on mitu toimingut
- Esiteks lähtestatakse järjekord nullini (st tühi).
- Määrake, kas järjekord on tühi või mitte.
- Määrake, kas järjekord on täis või mitte.
- Uue elemendi sisestamine tagumisest otsast (Enqueue).
- Elemendi kustutamine esiosast (Dequeue).
Järjekorda saab rakendada kahel viisil
- Staatiliselt (massiivide kasutamine)
- Dünaamiliselt (osade kasutamine)
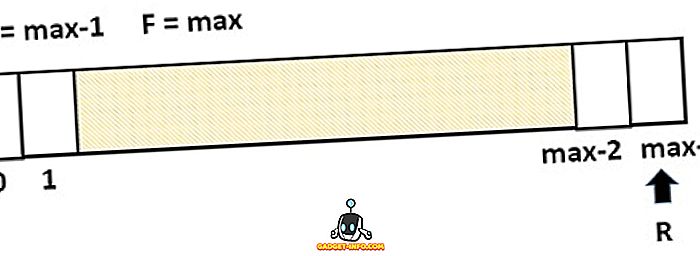
Lineaarse järjekorda piiramine on see, et see loob stsenaariumi, kus järjekorda ei saa lisada uut elementi isegi siis, kui järjekord sisaldab tühja ruumi. See ülaltoodud olukord on illustreeritud allpool toodud joonisel. Siin on tagaosa viimase indeksi suunas, samas kui kõik kastid on tühjad, uusi elemente ei saa lisada.
Ümmarguse järjekorra määratlus
Ümmargune järjekord on lineaarse järjekordi variant, mis ületab tõhusalt lineaarse järjekorda piiramise. Ümmarguses järjekorras lisatakse uus element järjekorra esimesele positsioonile, kui viimane on hõivatud ja ruumi on saadaval. Kui tegemist on lineaarse järjekorraga, võib sisestamise teha ainult tagumisest otsast ja kustutamist esiosast. Täielikus järjekorras pärast järjestikuste järjestikuste kustutamiste sooritamist tekib teatud olukord, kus ühtegi uut elementi ei saa lisada isegi siis, kui olemasolev ruum on allavoolu (taga = max - 1) veel olemas.
Ümmargune järjekord ühendab mõlemad otsad kursoriga, kus esimene element on pärast viimast elementi. Samuti jälgib see esi- ja tagaosa, rakendades mõningaid täiendavaid loogikaid, et oleks võimalik jälgida elemente, mis tuleb sisestada ja kustutada. Sellega ei tekita ümmargune järjekord ülevoolu seisundit enne, kui järjekord on tegelikus.
Mõned tingimused, millele järgneb ümmargune järjekord:
- Ees peab olema esimene element.
- Järjekord on tühi, kui esipaneel = taga.
- Uue elemendi lisamisel suurendatakse järjekorda ühe väärtusega (tagumine = tagumine + 1).
- Kui element kustutatakse järjekorrast, suurendatakse eesmist ühe võrra (eesmine = ees + 1).
Peamised erinevused lineaarse järjekorra ja ümmarguse järjekordade vahel
- Lineaarne järjekord on tellitud loend, milles andmeelemendid on järjestatud järjestuses. Seevastu ümmargune järjekord salvestab andmed ringikujuliselt.
- Lineaarne järjekord järgib FIFO järjekorda ülesande täitmiseks (esimeses asendis lisatud element kustutatakse esimeses asendis). Vastupidi, ringikujulises järjekorras võib elemendi toimingute järjekord muutuda.
- Elementide sisestamine ja kustutamine on fikseeritud lineaarses järjekorras, st lisamine tagumisest otsast ja kustutamine esiosast. Teisest küljest on ringjoont võimalik elementi sisestada ja kustutada mis tahes punktist, kuni see on vaba.
- Lineaarne järjekord raiskab mäluruumi, samas kui ümmargune järjekord muudab ruumi tõhusaks kasutamiseks.
Lineaarse järje rakendamine
Allpool toodud algoritm illustreerib elementide lisamist järjekorda:
Järjekorras on kolm andmemuutujat, mis sisaldavad ühte massiivi järjekorra salvestamiseks ja teine, et salvestada esi- ja tagumist algasendit -1.
sisestada (element, järjekord, n, taga) {if (taga == n) siis printida "järjekordne ülevool"; muu {taga = taga + 1; järjekord [tagumine] = kirje; }} Allpool toodud algoritm illustreerib elementide kustutamist järjekorras:
delete_circular (kirje, järjekord, taga, ees) {if (taga == ees) ja seejärel printige "järjekordne allavool"; muu {front = front + 1; kirje = järjekord [ees]; }} Ümmarguse järjekorda rakendamine
Algoritm elementi lisamise ümmarguses järjekorras tõlgendamiseks:
insert_circular (kirje, järjekord, taga, ees) {taga = (taga + 1) mod n; kui (ees == taga) siis printida "järjekord on täis"; other {queue [rear] = üksus; }} Algoritm selgitab elementi kustutamist ümmarguses järjekorras:
delete_circular (üksus, järjekord, taga, ees) {if (ees == taga) ja seejärel printimine ("järjekord on tühi"); muu {front = front + 1; kirje = järjekord [ees]; }} Järeldus
Lineaarne järjekord on mõningatel juhtudel ebaefektiivne, kui elemendid on vajalikud sisestusoperatsiooni läbiviimiseks vabade ruumide juurde liikumiseks. See on põhjus, miks ta kipub raiskama ruumi, samas kui ümmargune järjekord kasutab salvestusruumi asjakohaseks kasutamiseks, kuna elemendid lisatakse mis tahes asendisse, kui on tühi ruum.