Kui järjestus järgib teatud reeglit, nimetatakse seda progressiooniks. See ei ole täpselt sama kui seeria, mis on defineeritud kui järjestuse elementide summeerimine. Lugege artiklit, et teada saada olulist erinevust jada ja seeria vahel.
Võrdluskaart
| Võrdluse alus | Järjestus | Seeria |
|---|---|---|
| Tähendus | Järjestust kirjeldatakse kui teatud mustrit järgivate numbrite või objektide kogumit. | Seeria viitab järjestuse elementide summale. |
| Tellimus | Oluline | Mõnikord on oluline |
| Näide | 1, 3, 5, 7, 9, 11 .... n .. | 1 + 3 + 5 + 9 + 11 ... n .. |
Järjestuse määratlus
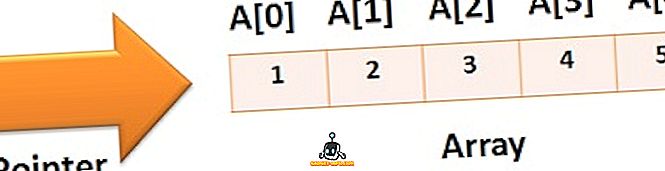
Matemaatikas tellitud objektide või numbrite kogum nagu a 1, a 2, a 3, a 4, a 5, a 6 …… a n…. väidetakse olevat järjestuses, kui teatud reeglina on sellel kindel väärtus. Järjestuse liikmeid nimetatakse terminiks või elemendiks, mis on võrdne füüsilise numbri mis tahes väärtusega. Iga järjestus on seotud eelmise ja järgneva ametiajaga. Üldiselt on järjestustel varjatud reeglid või muster, mis aitab teil teada saada järgmise ametiaja väärtusest.
N. Ametiaeg on täisarvu n (positiivne) funktsioon, mida loetakse järjestuse üldsõnaks. Järjestus võib olla piiratud või lõpmatu.
- Lõplik järjestus : piiratud järjestus on selline, mis peatub numbrite a 1, a 2, a 3, a 4, a 5, a 6 …… a n lõppu, mida esindab:

- Lõpmatu järjestus : Lõpmatu järjestus viitab järjestusele, mis on lõputu, a 1, a 2, a 3, a 4, a 5, a 6 …… a n…. ., esindab:

Seeria määratlus
Järjestuse (a n ) tingimuste lisamine on tuntud kui seeria. Sarnaselt järjestusele võib seeria olla ka piiratud või lõpmatu, kus piiratud seeria on selline, millel on piiratud arv termineid, mis on kirjutatud kui 1 + a 2 + a 3 + a 4 + a 5 + a 6 + …… a n . Erinevalt lõpmatusest seeriatest, kus elementide arv ei ole piiratud või mis on lõputud, kirjutatud kui 1 + a 2 + a 3 + a 4 + a 5 + a 6 + …… a n + ….
Kui a 1 + a 2 + a 3 + a 4 + a 5 + a 6 + …… a n = S n, siis S n loetakse seeria n elementide summaks. Mõistete summat esindab sageli kreeka täht sigma (Ʃ). Seega,

Järjestuse ja seeria põhilised erinevused
Järjestuse ja seeria erinevust saab selgelt tõendada järgmistel põhjustel:
- Järjestus on määratletud kui kindlat mustrit järgivate numbrite või objektide kogum. Kui järjestuse elemendid kokku liidetakse, tuntakse neid seeriana.
- Telli asjad järjestuses, kuna on olemas teatud reegel, mis näeb ette järjestuse mustri. Seega on 1, 2, 3th erinev 3, 1, 2-st. Teisest küljest võib aga välimuse järjekorras olla või mitte, nagu absoluutselt läheneva seeria puhul, ei ole järjekorras oluline. Niisiis on 1 + 2 + 3 sama kui 3 + 1 + 2, ainult nende järjestus on erinev.
Järeldus
Aritmeetiline progressioon (AP) ja geomeetriline progressioon (GP) on samuti järjestused, mitte seeriad. Aritmeetiline progressioon on järjestus, milles on tavaline erinevus järjestikuste terminite nagu 2, 4, 6, 8 ja nii edasi. Vastupidi, geomeetrilises progressioonis on järjestuse iga element eelmise mõiste ühine kordaja, nagu 3, 9, 27, 81 ja nii edasi. Sarnaselt on Fibonacci järjestus ka üks populaarsemaid lõpmatuid järjestusi, milles iga termin saadakse kahe eelneva terminiga 1, 1, 3, 5, 8, 13, 21 ja nii edasi.