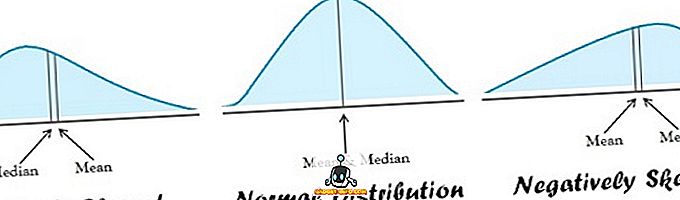
Keskmise tendentsi ideaalne mõõt on selline, mis on selgelt määratletud, kergesti mõistetav, lihtsalt arvutatav. See peaks põhinema kõikidel tähelepanekutel ja kõige vähem mõjutatud andmete kogumil esinevatest äärmuslikest tähelepanekutest.
Inimesed on need kaks meedet sageli vastandlikud, kuid tegelikult on need erinevad. See artikkel toob esile põhilised erinevused keskmiste ja mediaanide vahel. Vaata.
Võrdluskaart
| Võrdluse alus | Tähendab | Keskmine |
|---|---|---|
| Tähendus | Keskmine tähendab antud väärtuste või koguste kogumi lihtsat keskmist. | Keskmine on määratud väärtuste kesknumbrina. |
| Mis see on? | See on aritmeetiline keskmine. | See on positsiooniline keskmine. |
| Esindab | Andmekogumi raskuskese | Andmekogumi raskuskese Andmekogumi keskpunkt |
| Kohaldatavus | Normaalne jaotus | Pööratud jaotus |
| Võõrväärtused | Keskmine on tundlik kõrvalekallete suhtes. | Keskmine mediaan ei ole võõraste suhtes tundlik. |
| Arvutus | Keskmine arvutatakse, lisades kõik tähelepanekud ja jagades saadud väärtused vaatluste arvuga. | Mediaani arvutamiseks on andmekogum paigutatud kasvavas või kahanevas järjekorras, siis uue andmekogu keskele langev väärtus on mediaan. |
Keskmise mõiste
Keskmine on kesktendents, mida määratletakse väärtuste kogumi keskmisena. See esindab antud väärtuste vahemiku mudelit ja kõige levinumat väärtust. Seda saab arvutada nii diskreetselt kui ka pidevalt.
Keskmine on võrdne kõigi tähelepanekute summaga, mis on jagatud andmestiku tähelepanekute arvuga. Kui muutuja poolt arvutatud väärtus on võrdne, on ka selle keskmine. Keskmine võib olla kahte tüüpi, proovi keskmine (x mean) ja populatsiooni keskmine (µ). Seda saab arvutada antud valemiga:
- Aritmeetiline keskmine :

n = väärtuste arv - Diskreetse seeria puhul :

- Pidevate teenuste puhul :

A = eeldatav keskmine
C = Ühine jagaja
Mediani määratlus
Keskmine keskse tendentsi mõõtmine on mediaan, mida kasutatakse väärtuse jagamiseks kaheks võrdseks osaks, st suuremaks pooleks proovist, populatsioonist või tõenäosusjaotusest alumisest poolest. See on keskmisest kõige väärtuslikum väärtus, mis saavutatakse, kui tähelepanekud sorteeritakse kindlas järjekorras, kas kasvavas või kahanevas järjekorras.
Keskmine mediaani arvutamiseks tuleb kõigepealt korraldada vaatlused väikseimast kuni kõrgeimani või kõige madalamani, seejärel rakendada sobiv valem, vastavalt tingimustele, mis on toodud allpool:
- Kui vaatluste arv on kummaline :

- Kui vaatluste arv on isegi :

- Pidevate seeriate puhul :

c = eelmise mediaani klassi kumulatiivne sagedus
f = keskmine klassi sagedus
h = klassi laius
Keskmised ja keskmised erinevused
Märkimisväärsed erinevused keskmiste ja mediaanide vahel on esitatud allpool esitatud artiklis:
- Statistikas määratletakse keskmine väärtus antud väärtuste või koguste kogumina. Keskmine väärtus on tellitud väärtuste loendi keskmine number.
- Kui keskmine on aritmeetiline keskmine, on mediaan positsiooniline keskmine, sisuliselt määrab andmekogu positsioon mediaani väärtuse.
- Keskmine viitab andmekomplekti raskuskeskmele, samas kui mediaan tõstab esile andmekogu keskmise väärtuse.
- Keskmine on sobiv tavaliselt jaotatud andmetele. Teisest küljest on mediaan kõige parem, kui andmejaotus on kaldu.
- Keskmist mõju avaldab äärmuslik väärtus, mis ei ole keskmise mediaaniga.
- Keskmine arvutatakse, lisades kõik tähelepanekud ja jagades saadud väärtused vaatluste arvuga; tulemus on keskmine. Erinevalt mediaanist on andmekogum järjestatud kasvavas või kahanevas järjekorras, siis uue andmekogu keskele langev väärtus on mediaan.
Näide
Leidke antud andmekogumite keskmine ja mediaan:
58, 26, 65, 34, 78, 44, 96
Lahendus: Arvutuse arvutamiseks peate jagama vaatluste summa tähelepanekute arvuga,

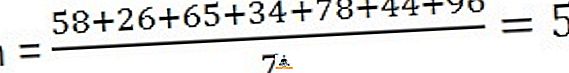
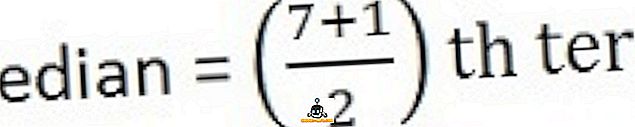
Et arvutada mediaan, kõigepealt korraldage seeria järjestuses, st madalaimast kuni kõrgeima,
26, 34, 44, 58, 65, 78, 96
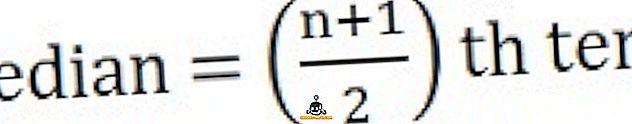
Järeldus
Pärast ülaltoodud punktide ülevaatamist võime öelda, et need kaks matemaatilist mõistet on erinevad. Aritmeetiline keskmine või keskmine loetakse keskse tendentsi parimaks mõõduks, kuna see sisaldab kõiki ideaalse mõõtme omadusi, kuid tal on üks puudus, et proovivõtukõikumised mõjutavad keskmist.
Samamoodi on ka mediaan üheselt määratletud ja kergesti mõistetav ning arvutatav ning selle meetme puhul on parim, et proovivõtu kõikumised seda ei mõjuta, kuid mediaani ainus puudus on see, et see ei põhine kõigil tähelepanekuid. Avatud lõpp-klassifikatsiooni puhul eelistatakse keskmist keskmist.















