Niisiis on lihtintressiks summa, mida makstakse kulutatud raha kasutamise eest kindla ajavahemiku jooksul. Teisest küljest, kui intressi tuleb tasuda, lisatakse see printsipaalile, kellele arvestatakse järgneva perioodi intressi, mida nimetatakse liitintressiks . Niisiis, siin käesolevas artiklis leiad põhilised erinevused lihtsate intresside ja liitintresside vahel, mille oleme koostanud pärast põhjalikku uurimist kahe termini kohta.
Võrdluskaart
| Võrdluse alus | Lihtne huvi | Kombineeritud intress |
|---|---|---|
| Tähendus | Antud intress tähendab intressi, mis arvutatakse protsendina põhisummast. | Kombineeritud intress on intress, mis arvutatakse protsendina põhiosast ja kogunenud intressist. |
| Tagasi | Vähem | Võrreldes kõrge |
| Põhisumma | Konstant | Muutub kogu laenuperioodi jooksul. |
| Kasv | Jääb ühtlaseks | Suureneb kiiresti |
| Intress on tasutud | Põhisumma | Põhisumma + kogunenud intress |
| Valem | Lihtne intress = P * r * n | Ühendi intress = P * (1 + r) ^ nk |
Lihtsate huvide mõiste
Lihtne Intress on intress, mida võetakse laenu- või põhiosa protsendina kogu laenuperioodi jooksul. Intress on raha kasutamise eest makstud hind või raha laekumisel saadud tulu. Laenu või laenatud summa intresside arvutamiseks on kõige lihtsam ja kiirem meetod. Kõige tavalisem näide lihtsast intressist on auto laen, kus intressi tuleb maksta ainult laenatud või laenatud algsest summast. Intressimäära arvutamiseks kasutatakse järgmist valemit:
Valem : lihtne intress = P × i × n
Kus P = põhisumma
i = intressimäär
n = aastate arv
Näiteks : kui laenate Rs. 1000 sõbra @ 10% aastas 3 aastat, siis peate tagastama Rs.1300 oma sõbra 3. aasta Rs 1000-le printsipaalile R ja Rs. 300 kui intressi, summa hoidmise eest. Kui me lisame põhisumma ja intressid, siis tuntakse seda kui summat. Üks asi tuleb meeles pidada, seda rohkem on raha ja perioodid, seda suurem on huvi.
Ühendi intresside mõiste
Kombineeritud intress on intress, mis arvutatakse protsendina muudetud põhisummast, st esialgne põhisumma koos eelnevate perioodide kogunenud intressiga. Selle meetodi puhul võtame kokku eelmistel aastatel algse põhisumma teenitud intressid, suurendades seega põhisummat, mille eest tasutakse järgmise perioodi intress. Siinkohal tuleb maksta intressi põhiosa eest ja laenu tähtaja jooksul kogunenud intresse.
Kahe intressimakse perioodi vaheline ajavahemik on tuntud kui konversiooniperiood. Konversiooniperioodi lõpus lisatakse intress, nagu:
| Konversiooniperiood | Liidetud |
|---|---|
| 1 päev | Iga päev |
| 1 nädal | Nädala |
| 1 kuu | Igakuine |
| 3 kuud | Kord kvartalis |
| 6 kuud | Poolaasta jooksul |
| 12 kuud | Aastas |
Tavaliselt maksavad pangad intresse poole aasta tagant, kuid finantseerimisasutustel on kord kvartalis intressi maksmise poliitika. Koondintresside arvutamiseks peate kasutama seda valemit:
Valem : Ühendi intress = P {(1 + i) n - 1}
Kus, P = peamine
n = aastate arv
i = intressi määr perioodi kohta
Peamised erinevused lihtsate intresside ja liitintresside vahel
Järgnevalt on toodud peamised erinevused lihtintresside ja liitintresside vahel:
- Põhisumma eest kogu laenuperioodi eest makstavat intressi tuntakse lihtsa intressina. Nii põhiosa kui ka varem teenitud intressi kohta arvutatud intressi tuntakse liitintressidena.
- Kombineeritud intress annab lihtsa intressiga võrreldes suure tulu.
- Lihthuvi puhul jääb printsipaal püsivaks, samal ajal kui liitintressi puhul muutub põhisumma liitumise mõju tõttu.
- Lihtsate intresside kasvumäär on madalam kui liitintress.
- Lihtsate intresside arvutamine on lihtne, samas kui liitintresside arvutamine on keeruline.
Video: Lihtne Vs
Näide
Oletame, et Alex hoiule Rs. 1000-le pangale 5% intressiga (lihtne ja ühend) pa 3 aastat. Uuri välja kogu huvi, mida ta saab kolmanda aasta lõpus?
Lahendus : siin P = 1000, r = 5% ja t = 3 aastat
Lihtne huvi =
Ühendi huvi =
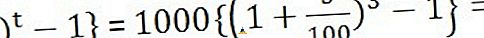
Järeldus
Intress on kellegi teise raha kasutamise tasu. Intressi, näiteks raha, inflatsiooni, alternatiivkulude ja riskiteguri maksmiseks on palju põhjuseid. Lihtne huvi on kiire arvutamine, kuid kombineeritud intress on praktiliselt raske. Kui arvutate nii lihtsa intressi kui ka intressi, mis on antud põhisumma, intressimäära ja aja kohta, leiad alati, et liitintress on alati suurem kui lihthuvi, mis tuleneb selle lisandumisest.
