
Sorteerimine on põhitoiming, milles massiivi elemendid on paigutatud teatud kindlas järjekorras, et suurendada selle otsitavust. Lihtsamalt öeldes sorteeritakse andmed nii, et neid oleks lihtne otsida.
Võrdluskaart
| Võrdluse alus | Sisestamise sorteerimine | Valik Sorteeri |
|---|---|---|
| Põhiline | Andmed sorteeritakse, sisestades andmed olemasolevasse sorteeritud faili. | Andmed sorteeritakse, valides ja paigutades järjestikused elemendid järjestatud asukohta. |
| Loodus | Stabiilne | Ebastabiilne |
| Protsess, mida tuleb järgida | Elemendid on eelnevalt tuntud, kui nende asukohta otsitakse. | Asukoht on varem teada, kui elemente otsitakse. |
| Kohene teave | Lisamise sorteerimine on elus sorteerimise tehnika, millega saab tegeleda koheste andmetega. | See ei saa otseste andmetega tegeleda, see peab olema alguses olemas. |
| Parim juhtumi keerukus | O (n) | O (n 2 ) |
Sisestamise määratlus
Sisestamise sorteerimine toimib, lisades väärtuste kogumi olemasolevasse sorteeritud faili. See konstrueerib sorteeritud massiivi, sisestades korraga ühe elemendi. See protsess jätkub, kuni kogu massiiv on järjestatud. Sisestamise sorti peamine kontseptsioon on iga elemendi lisamine lõplikku nimekirja sobivasse kohta. Sisestusviis salvestab efektiivse koguse mälu.
Sisestamise sorteerimine
- See kasutab kahte rida massiive, kus üks salvestab sorteeritud andmed ja muud sortimata andmetele.
- Sorteerimisalgoritm toimib seni, kuni sortimata komplekti elemente on.
- Oletame, et massiivis on 'n' arv elemente. Esialgu on sort 0-ga element (LB = 0) sorteeritud komplektis. Ülejäänud elemendid on loendi sortimata sektsioonis.
- Sorteerimata osa esimesel elemendil on massiindeks 1 (kui LB = 0).
- Pärast iga iteratsiooni valib ta sorteerimata partitsiooni esimese elemendi ja lisab selle sorteeritud komplekti õigesse kohta.
Sisestamise eelised
- Lihtne rakendada ja väga tõhus, kui seda kasutatakse väikeste andmekogumitega.
- Täiendav mäluruumi nõue sisestamise sortide kohta on väiksem (st O (1)).
- Seda loetakse elusat sorteerimistehnikaks, kuna loendit saab sorteerida uute elementide vastuvõtmisel.
- See on kiirem kui muud sorteerimisalgoritmid.
Näide:
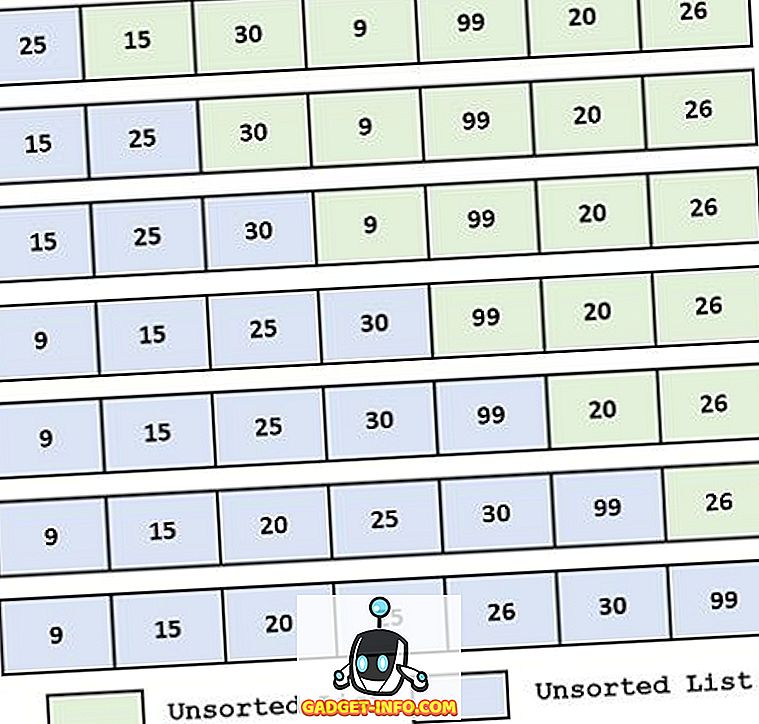
Valiku määratlus Sorteeri
Valik sorteerib läbi sorteerimise, otsides minimaalse väärtuse numbri ja paigutades selle vastavalt esimesele või viimasele positsioonile vastavalt järjestusele (kasvavalt või kahanevalt). Minimaalse võtme otsimise ja õigesse asendisse paigutamise protsessi jätkatakse seni, kuni kõik elemendid on õiges asendis.
Valiku sorteerimine
- Oletame, et mälus on massiiv ARR koos N-elementidega.
- Esimesel käigul otsitakse väikseimat võtit koos selle asendiga ja ARR [POS] vahetatakse ARR-ga [0]. Seetõttu on ARR [0] sorteeritud.
- Teises läbisõidul määratakse uuesti väikseima väärtuse positsioon N-1 elementide alamrubriigis. Vahetage ARR [POS] ARR-ga [1].
- N-1 läbimisel viiakse läbi sama protsess, et sorteerida N-elementide arv.
Näide:
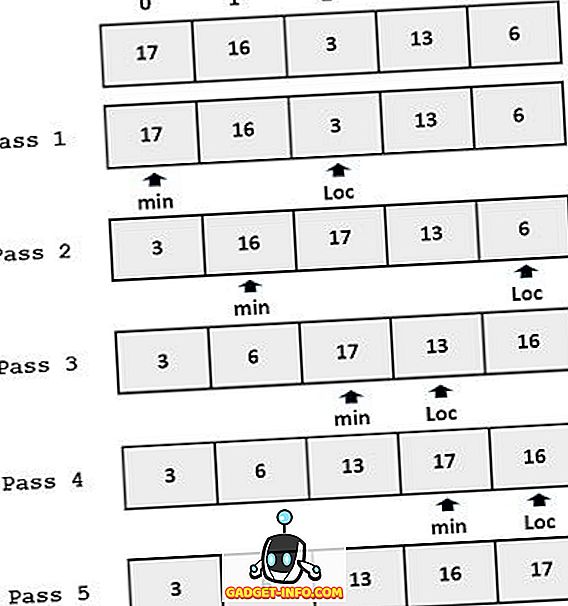
Sisestamise sorteerimise ja valiku vahelised peamised erinevused Sorteeri
- Sisestusviis täidab tavaliselt sisestust. Vastupidi, valikuklass teostab nõutavate elementide valiku ja asukoha.
- Lisamise sort on stabiilne, samas kui valiku sort ei ole stabiilne algoritm.
- Sisestamise sorteerimise algoritmi puhul on elemendid eelnevalt tuntud. Seevastu valiku sort sisaldab eelnevalt asukohta.
- Sisestusviis on elus sorteerimise tehnika, kus saabuvad elemendid sorteeritakse kohe nimekirjas, samas kui valikute sort ei suuda koheseid andmeid korralikult töötada.
- Sisestusliigil on parimal juhul O (n) tööaeg. Vastupidi, valiku sorteerimise parim juhtumikordaja on O (n2).
Sisestamise keerukus
Sisestamise sorteerimise parimaks keerukuseks on O (n) ajad, st kui massiiv on varem sorteeritud. Samamoodi, kui massiivi sorteeritakse vastupidises järjekorras, võrreldakse sorteerimata massiivi esimest elementi sorteeritud komplekti iga elemendiga. Niisiis, halvimal juhul on sisestamise sorti jooksuaeg ruutkeskne, st O (n2) . Keskmiselt peab see tegema ka minimaalse (k-1) / 2 võrdluse. Seega on keskmisel juhul ka ruutkeskmine tööaeg O (n2).
Valiku keerukus Sorteeri
Kuna valiku, sorteerimise töö ei sõltu massiivi elementide algsest järjestusest, ei ole parimate juhtumite ja valiku sorteerimise halvima keerukuse vahel suur erinevus.
Valikuvalik valib minimaalse väärtuse elemendi, valikuprotsessis skaneeritakse kõik n 'elementide arv; seepärast tehakse esimeses passis n-1 võrdlusi. Seejärel vahetatakse elemente. Sarnaselt teisele läbipääsule, et leida ka teine väikseim element, vajame ülejäänud n-1 elementide skaneerimist ja protsessi jätkatakse kuni kogu massiivi sortimiseni.
Seega on valiku sortide tööaja keerukus O (n2) .
= (n-1) + (n-2) + ……… .. + 2 + 1
= n (n-1) / 2 = O (n2)
Järeldus
Mõlema sorteerimisalgoritmi hulgas on sisestamise sort kiire, tõhus, stabiilne, samal ajal kui valik sortimine toimib tõhusalt ainult siis, kui on tegemist väikese elementide kogumiga või nimekiri on osaliselt eelnevalt sorteeritud. Valiku sortimisega tehtud võrdluste arv on suurem kui teostatud liikumised, samas kui sisestamisel sorteeritakse elementide arvu või vahetuse arv on suurem kui tehtud võrdlused.









