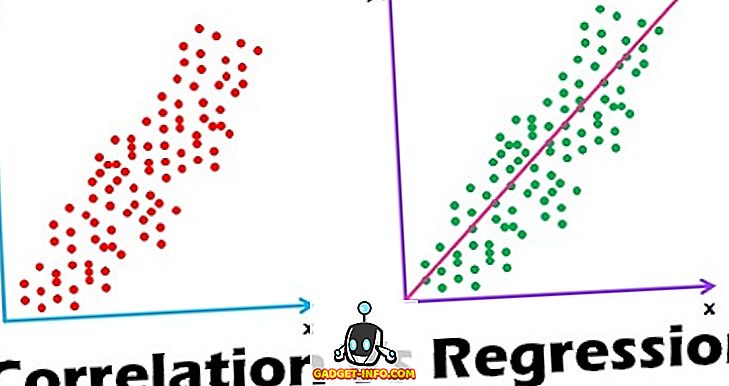
Erinevus korrelatsiooni ja regressiooni vahel on intervjuudes üheks kõige sagedamini küsitavaks küsimuseks. Veelgi enam, paljud inimesed mõistavad nende kahe mõistmisel ebaselgust. Niisiis, lugege täielikult sellest artiklist, et teil oleks selge arusaam nendest kahest.
Võrdluskaart
| Võrdluse alus | Korrelatsioon | Regressioon |
|---|---|---|
| Tähendus | Korrelatsioon on statistiline meede, mis määrab kahe muutuja koosmõju või seose. | Regressioon kirjeldab, kuidas sõltumatu muutuja sõltub sõltuvalt muutujast. |
| Kasutamine | Esitada lineaarne suhe kahe muutuja vahel. | Parima joone sobitamine ja ühe muutuja hindamine teise muutuja alusel. |
| Sõltuvad ja sõltumatud muutujad | Erinevust pole | Mõlemad muutujad on erinevad. |
| Näitab | Korrelatsioonikoefitsient näitab, mil määral kaks muutujat liiguvad. | Regressioon näitab ühiku muutuse mõju teadaolevas muutuja (x) muutujale (y). |
| Eesmärk | Et leida arvnäitajat, mis väljendab muutujate vahelist suhet. | Hinnata juhusliku muutuja väärtusi fikseeritud muutuja väärtuste alusel. |
Korrelatsiooni määratlus
Termin "korrelatsioon" on kahe sõna "Co" (koos) ja kahe koguse vahelise seose kombinatsioon. Korrelatsioon on siis, kui kahe muutuja uurimise ajal täheldatakse, et ühe muutuja ühiku muutus on samaväärse muudatusega, st otsese või kaudse muutusega. Või siis öeldakse, et muutujad on korrelatsioonita, kui ühe muutuja liikumine ei tähenda mingis teises liikumises kindlas suunas. See on statistiline meetod, mis esindab muutujate paaride vahelise seose tugevust.
Korrelatsioon võib olla positiivne või negatiivne. Kui kaks muutujat liiguvad samas suunas, st ühe muutuja suurenemine toob kaasa teise muutuja vastava suurenemise ja vastupidi, loetakse muutujad positiivselt korrelatsiooniks. Näiteks : kasum ja investeeringud.
Vastupidi, kui need kaks muutujat liiguvad erinevates suundades, nii et ühe muutuja suurenemine toob kaasa teise muutuja vähenemise ja vastupidi, on see olukord tuntud kui negatiivne korrelatsioon. Näiteks : toote hind ja nõudlus.
Korrelatsioonimeetmed on esitatud järgmiselt:
- Karl Pearsoni tootemomendi korrelatsioonikoefitsient
- Spearmani auaste korrelatsioonikoefitsient
- Scatter diagramm
- Samaaegsete kõrvalekallete koefitsient
Regressiooni mõiste
Statistilist meetodit, mis võimaldab hinnata ühe või mitme sõltumatu muutuja muutusest tulenevat muutust metrilisest sõltuvast muutujast kahe või enama muutuja keskmise matemaatilise suhte põhjal, tuntakse regressioonina. See mängib olulist rolli paljudes inimtegevustes, kuna see on võimas ja paindlik vahend, mis kasutas mineviku, praeguse või tulevase sündmuse prognoosimiseks varasemaid või praeguseid sündmusi. Näiteks : Varasemate andmete põhjal saab hinnata ettevõtte tulevast kasumit.
Lihtsas lineaarses regressioonis on kaks muutujat x ja y, kus y sõltub x-st või öelda, mida mõjutab x. Siin nimetatakse y sõltuvaks või kriteeriumi muutuja ja x on sõltumatu või ennustatav muutuja. Y regressioonirida x-s on väljendatud allpool:
y = a + bx
kus, a = konstant,
b = regressioonikoefitsient,
Selles võrrandis on a ja b kaks regressiooniparameetrit.
Peamised erinevused korrelatsiooni ja regressiooni vahel
Allpool toodud punktid selgitavad üksikasjalikult korrelatsiooni ja regressiooni erinevust:
- Statistilist mõõdet, mis määrab kahe koguse koosmõju või seost, nimetatakse korrelatsiooniks. Regressioon kirjeldab, kuidas sõltumatu muutuja sõltub sõltuvalt muutujast.
- Korrelatsiooni kasutatakse kahe muutuja vahelise lineaarse suhte esindamiseks. Vastupidi, regressiooni kasutatakse parimate joonte sobitamiseks ja ühe muutuja hindamiseks teise muutuja alusel.
- Korrelatsioonis puudub sõltuvus sõltuvate ja sõltumatute muutujate vahel, st korrelatsioon x ja y vahel on sarnane y ja x omaga. Vastupidi, y x regressioon erineb x-st y-st.
- Korrelatsioon näitab muutujate vahelise seose tugevust. Vastupidiselt sellele kajastab regressioon üksuse muutuse mõju sõltuvale muutujale sõltuvale muutujale.
- Korrelatsiooni eesmärk on leida arvuline väärtus, mis väljendab muutujate suhet. Erinevalt regressioonist, mille eesmärgiks on juhusliku muutuja väärtuste prognoosimine fikseeritud muutuja väärtuste alusel.
Järeldus
Eespool toodud aruteluga on ilmne, et nende kahe matemaatilise kontseptsiooni vahel on suur erinevus, kuigi neid kahte uuritakse koos. Korrelatsiooni kasutatakse siis, kui teadlane soovib teada, kas uuritavad muutujad on omavahel seotud või mitte, kui jah, siis milline on nende seose tugevus. Parimat korrelatsiooni mõõdet peetakse Pearsoni korrelatsioonikoefitsiendiks. Regressioonianalüüsis luuakse funktsionaalne suhe kahe muutuja vahel, et tulevikus prognoosida sündmusi.